By Aarib Zaidi
We frequently hear about two schools of thinking in statistics: Frequentist and Bayesian. At the most fundamental level, the distinction between these two methods arises from how they understand probability. A frequentist defines probability as the limited frequency with which an event occurs, but a Bayesian statistician defines probability as the degree of belief in the event’s occurrence. Overall, these alternating interpretations of probability have resulted in distinct approaches to statistical modelling and inference, with Bayesian techniques incorporating previous beliefs and information through the use of prior distributions whereas frequentist methods depend fully upon the data available (Verma, 2017).
Moving on, Bayesian Networks are a powerful tool used in statistics, machine learning and AI for modelling uncertain circumstances. These networks offer a graphical representation of probabilistic relationships among variables, making them an essential feature of decision support systems, machine learning and diagnostic systems. In this article, we are going to delve deep into the intricacies of Bayesian Networks; exploring their structure, components, applications and drawbacks.
1) Structure and Components of Bayesian Networks
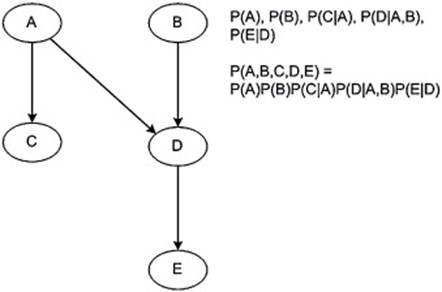
A Bayesian Network is a probabilistic graphical model, in the form of a directed acrylic graph (DAG), where nodes represent variables and edges represent causal dependencies among the variables.
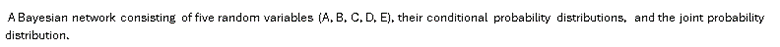
1.1 Nodes and Keys
The key components of the Bayesian Network are:
- Nodes represent a variable, such as an individual’s age or height. This means that the variable can be either continuous or discrete.
- Edges display the casual or conditional dependencies among the variables. For example, an edge from Node A to Node D implies that A has a direct impact on D (Nesma & Wassal, 2015).
1.2 – CPTs
Conditional Probability Tables are defined for a set of random variables in which every node is connected a CPT. Essentially, the CPT helps display the conditional probabilities of a single variable with respect to the others (Noriega et al.). For a node 𝑋 with parents 𝑃a (𝑋), the CPT provides the probability distribution P(X ∣ Pa(X)).
1.3 – Joint Probability Distribution
In the Bayesian Network, all variables are encoded with a joint probability distribution. This JPD is the corresponding probability distribution on all possible pairs of outputs. Also, the JPD can be decomposed into the conditional probability distribution specified by the CPTs (see above). For example, if the variables in a series are X1,X2,…,Xn , the joint distribution is given by: P (X1,X2,…,Xn) = ∏ni=1 P(Xi ∣ Pa(Xi))
2) Learning Bayesian Networks
The process of learning Bayesian Networks revolves around determining the parameters and structures of the network from data. This can be further simplified into the two following stages:
2.1 Structure Learning
Structural learning is the process by which data is processed in order to learn the links of a Bayesian network as well as being able to identify the DAG that can best represent the intricate dependencies among the various variables. Overall, there are two types of structural learning:
-Score-Based Methods involves the evaluation of different network structures using a scoring function that records how well a data structure fits the observed data.
– Constraint-Based Methods are methods that use statistical tests to identify conditional independencies among variables, something that can then be utilized to infer the network structure.
2.2- Parameter Learning
Once the structure is determined, data is used to learn the distribution of a Bayesian Network. This can be done using:
- Maximum Likelihood Estimation (MLE) estimates the parameters that maximize the likelihood of the observed data given the network structure.
- Bayesian Estimation incorporates prior distributions across the parameters and update them based upon observed data.
3. Inference in Bayesian Networks
Inference is essentially the process that a trained machine learning model uses to draw conclusions from brand-new data. There are several methods for inference:
3.1-Exact Inference
An exact inference algorithm codes for the exact posterior probabilities. Common examples include:
- Variable elimination involves an algorithm eliminating the variables by summing up their possible values to compute marginal distributions.
- Belief Propagation (also called the Sum-Product algorithm) operates through factor graphs in which messages are passed between nodes to compute for both marginal and joint probabilities.
- Junction Tree Algorithm is a more organised strategy that transforms the Bayesian Network into a tree structured called a ‘junction tree’. In it, each node holds a subset of variables, which when put together form a full subgraph in the network (Suraj, 2024).
3.2-Approximate Inference
An approximate inference method will be used when the exact inference is computationally infeasible and will aid in providing approximate solutions (Nikhil, 2024). A few techniques include:
- Monte Carlo Methods, such as the Markov Chaine Monte Carlo (MCMC) create samples from the posterior distributions and help estimate probabilities.
- Variational Inference approximates the posterior distribution through a simpler distrubtion and optimizes the parameters of this approximation (Ramesh, 2024).
4. The Applications of Bayesian Networks
Bayesian Networks are widely used in various domains around the world:
4.1- Medical Diagnosis
In medical diagnosis, Bayesian Networks model the probabilistic relationships between symptoms, diseases and test results. This then helps in predicting the likelihood of a specific person having a disease through their observed symptoms and test outcomes. Overall, this aids in swift and personalized healthcare plans (MCLachlan et al., 2020).
4.2 Decision Support Systems
Bayesian Networks are also used in decision support systems due to them being able to assess risks, make predictions and being able to evaluate the probable outcomes of a decision. All of this helps in modeling complex decision-making scenarios involving uncertainty.
4.3 Machine Learning and Data Mining
In machine learning, Bayesian Networks are used in classification, clustering and anomaly detection. This helps to provide a framework for incorporating prior knowledge and dealing with data that has gone missing.
5. Challenges and Future Directions
Despite the many advantages of Bayesian Networks, there remain a few drawbacks. Some of these include:
5.1- Scalability
As the number of variables increases, the algorithm increases in complexity and the computational requirements for inference drastically increase. Therefore, efficient algorithms are needed to handle large-scale networks.
5.2-Learning from Sparse Data
On many occasions, the issue arises that data is either sparse in number or is incomplete. Therefore, learning accurate structures and parameters from them is challenging. Therefore, advances in techniques for handling missing data and incorporating domain knowledge are critical.
5.3-Integration with Other Models
Integrating a Bayesian Network with other probabilistic models and machine learning techniques (e.g. deep learning) may be hard and therefore remains an active point of research. Hence, hybrid models which leverage the strengths of different approaches are currently under development (Laura, 2007).
Conclusion
Overall, Bayesian Networks offer a robust framework through which data can be modelled and reasoned in a graphical model. This allows for efficient reasoning under uncertainty, being able to represent complex dependencies and performing inference makes them an invaluable tool in a multitude of real-world applications. Despite its challenges, our ongoing research ensures that Bayesian Networks remains inherently relevant in the ever evolving landscape of data science and Artificial Intelligence.
Works Cited
Ahmad, Imad . “Top 10 Real-World Bayesian Network Applications – Know the Importance!” DataFlair, 26 Aug. 2017, data-flair.training/blogs/bayesian-network-applications/.
“Bayesian Network – an Overview | ScienceDirect Topics.” Www.sciencedirect.com, www.sciencedirect.com/topics/mathematics/bayesian-network.
Belenguer-Llorens, Albert, et al. “A Novel Bayesian Linear Regression Model for the Analysis of Neuroimaging Data.” Applied Sciences, vol. 12, no. 5, 1 Mar. 2022, pp. 2571–2571, www.mdpi.com/2076-3417/12/5/2571, https://doi.org/10.3390/app12052571.
Janu Verma. “Linear Regression: Frequentist and Bayesian.” Medium, Markovian Labs, 8 Feb. 2017, medium.com/markovian-labs/linear-regression-frequentist-and-bayesian-447f97c8d330.
McLachlan, Scott, et al. “Bayesian Networks in Healthcare: Distribution by Medical Condition.” Artificial Intelligence in Medicine, June 2020, p. 101912, https://doi.org/10.1016/j.artmed.2020.101912.
Nikhil. “Approximate & Exact Inference in Bayesian Networks – Nikhil – Medium.” Medium, Medium, 4 July 2022, nikhil-st8.medium.com/approximate-exact-inference-in-bayesian-networks-b682ed19fbbf. Accessed 17 Aug. 2024.
Parameter Learning. 2017.
Ramesh. “Approximate Inference in Bayesian Networks.” GeeksforGeeks, GeeksforGeeks, 30 May 2024, www.geeksforgeeks.org/approximate-inference-in-bayesian-networks/. Accessed 17 Aug. 2024.
Ramírez Noriega, Alan, et al. “Construction of Conditional Probability Tables of Bayesian Networks Using Ontologies and Wikipedia.” Computación Y Sistemas, vol. 23, no. 4, 1 Dec. 2019, pp. 1275–1289, www.scielo.org.mx/scielo.php?pid=S1405-55462019000401275&script=sci_arttext&tlng=en, https://doi.org/10.13053/cys-23-4-2705.
“Research Challenges Faced in Bayesian Networks Projects.” Network Simulation Tools, 2 Mar. 2021, networksimulationtools.com/bayesian-networks-projects/. Accessed 17 Aug. 2024.
“Structural Learning | Bayes Server.” Bayesserver.com, 2024, bayesserver.com/docs/learning/structural-learning/#:~:text=Structural%20learning%20is%20the%20process. Accessed 10 Aug. 2024.
“Structure Learning – an Overview | ScienceDirect Topics.” Www.sciencedirect.com, www.sciencedirect.com/topics/mathematics/structure-learning.
Suraj. “Exact Inference in Bayesian Networks.” GeeksforGeeks, 30 May 2024, www.geeksforgeeks.org/exact-inference-in-bayesian-networks/.
Uusitalo, Laura. “Advantages and Challenges of Bayesian Networks in Environmental Modelling.” Ecological Modelling, vol. 203, no. 3-4, May 2007, pp. 312–318, https://doi.org/10.1016/j.ecolmodel.2006.11.033.
Wikipedia Contributors. “Bayesian Linear Regression.” Wikipedia, Wikimedia Foundation, 9 Aug. 2024, en.wikipedia.org/wiki/Bayesian_linear_regression#:~:text=Bayesian%20linear%20regression%20is%20a. Accessed 10 Aug. 2024.
Wundervald, Bruna . Bayesian Linear Regression. June 2019, www.researchgate.net/publication/333917874_Bayesian_Linear_Regression.